The CG of a Can of Beer

Aside from providing the solution to an amusing puzzle, this page is primarily an exercise in the use of HTML5 MathML for math expressions. MathML is supported by most modern web browsers, but the quality of the rendering may vary.

Firefox (version 31.0, at the time of this writing) does a rather good job, probably the best of most current browsers.

I may also use this page as a test case for responsive web design.

Problem statement

When a can of beer is full the center of gravity is at the center of the can. As the beer is consumed the center of gravity moves down. When the can is finally empty the center of gravity is back at the center. At what point does the center of gravity reach its lowest point and start turning up again?

We will assume that the can is a uniform cylinder and that we are only concerned with its center of gravity when it is sitting upright. We will assume that the gravitational field is constant over the height of the can, so we may consider the center of mass to be equivalent to the center of gravity.

Solution

Let

2 h = The height of the can,

m_{b} = The mass of the beer,

m_{c} = The mass of the can, and

k = \frac{m_{b}}{m_{c}}

If we define x, where 0 ≤ x ≤ 1, as the proportion of beer remaining in the can, and we define y, where 0 ≤ y ≤ 1, as the height of the center of mass of the can and the beer together, as a proportion of the height of the center of mass of the can alone, then

h = the height of the center of mass of the can,

h x = the height of the center of mass of the beer,

h y = the height of the center of mass of the beer and can, and

m_{b} x = the mass of the beer remaining in the can.

Figure 1. Center of gravity (mass) of a can of beer.

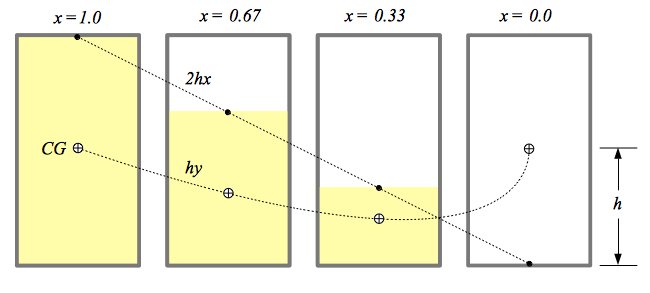
The mass times the distance of the center of mass (from the base of the can, in this case) is sometimes called the "mass moment". The mass moment of the beer and the can together must be equal to the mass moment of the beer plus the mass moment of the can:

h y (m_{b} x + m_{c}) = h x m_{b} x + h m_{c}

That is another way of saying that the height of the center of mass of the beer and can together is the mass-weighted average of the height of the center of mass of the beer and the height of the center of mass of the can.

Solving for y,

y (m_{b} x + m_{c}) = m_{b} x^{2} + m_{c}

y (\frac{m_{b}}{m_{c}} x + 1) = \frac{m_{b}}{m_{c}} x^{2} + 1

y (k x + 1) = k x^{2} + 1

y = \frac{k x^{2} + 1}{k x + 1}

That function tells us how the center of mass moves as the beer is consumed. The shape of the curve depends on the ratio k of the initial mass of the beer to the mass of the can.

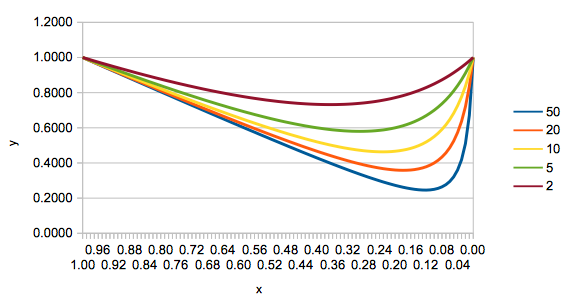
Figure 2. Variation in the height of the center of mass as a function of the proportion of beer remaining, for several values of k.

y reaches a minimum when its derivative goes to zero. Differentiating,

\frac{d y}{d x} = \frac{k (k x^{2} + 2 x - 1)}{{(k x + 1)}^{2}}

It can be seen that the derivative is zero when $k x^{2} + 2 x - 1 = 0$ .
The positive solution for that polynomial is the proportion of beer left when the center of mass is at its lowest level. Using the quadratic formula,

x = \frac{- 2 + \sqrt{4 + 4 k}}{2 k}

Which simplifies to

x = \frac{\sqrt{k + 1} - 1}{k}

For a typical 12-ounce aluminum beer can, the mass of the beer is about 10 times the mass of the can (k = 10), so the center of mass is at its lowest when there is slightly less than one-quarter of the beer remaining in the can:

x = \frac{\sqrt{11} - 1}{10} \approx 0.23

Alternative solution

We can find the minimum without using calculus by making the observation that the center of mass will be going down as long as we are removing beer that is above it and the center of mass will start going up when we begin removing beer below it. In other words, the center of mass will be at its lowest when it coincides with the surface of the beer. At that point,

y h = 2 h x

, so if we substitute

2 x

for y in the mass moment equation,

2 x h (m_{b} x + m_{c}) = x h m_{b} x + m_{c} h

and simplify, we get the same polynomial as before, without having to use a derivative:

2 x (k x + 1) = k x^{2} + 1

2 k x^{2} + 2 x = k x^{2} + 1

k x^{2} + 2 x - 1 = 0

Cheers!